Rumus Segitiga Luas dan Keliling - Pernahkah kalian mengamati atap rumah kalian? Perhatikan contoh atap rumah di bawah ini.
Berbentuk apakah salah satu sisi atap rumah tersebut? Jika kalian menjawab segitiga, maka jawaban kalian sudah tepat. Namun, tahukah kalian apa itu segitiga? Tahukah kalian apa saja jenis-jenis dari segitiga? Bagaimana cara untuk menentukan keliling dan luas segitiga. Untuk menjawab pertanyaan-pertanyaan itu, pelajarilah materi segitiga berikut dengan baik.
Segitiga dapat didefinisikan sebagai berikut.
Ruas-ruas garis yang terdapat dalam segitiga dikenal sebagai sisi-sisi segitiga. Adapun biasanya segitiga dilambangkan dengan “ △”. Perhatikan gambar di bawah ini.
Gambar di atas merupakan salah satu contoh segitiga dan diberi nama segitiga ABC atau ditulis △ABC. Pada △ABC, sisi-sisi pembentuk segitiga tersebut antara lain sisi AB, sisi BC, dan sisi AC. Selain dibentuk oleh tiga sisi tersebut, sebuah segitiga juga memiliki sudut-sudut yang banyaknya tiga buah. Pada △ABC, sudut-sudutnya adalah:
Keliling segitiga adalah jumlah panjang dari ketiga sisi yang dimiliki oleh sebuah segitiga. Perhatikan △ABC di bawah ini.
Misalkan panjang sisi AB adalah c, panjang sisi BC adalah a, dan panjang sisi AC adalah b, maka keliling △ABC di atas dapat dirumuskan sebagai berikut.
Keliling △ABC = AB+BC+AC
K = sisi c + sisi a + sisi b
= sisi a + sisi b + sisi c
Dari hal tersebut, keliling dari sebuah segitiga dengan panjang sisi a cm, b cm, dan c cm dapat dirumuskan dengan:
Rumus keliling segitiga ini berlaku untuk menghitung keliling semua jenis segitiga baik itu segitiga sama kaki, segitiga sama sisi, segitiga sembarang, segitiga siku-siku, segitiga lancip dan segitiga tumpul.
Contoh Soal Keliling Segitiga:
Tentukan keliling segitiga yang panjang sisinya 12 cm, 5 cm, dan 13 cm!
Jawab:
Diketahui panjang sisi segitiga adalah 12 cm, 8 cm, dan 10 cm, maka apabila digambarkan menjadi:
Keliling Segitiga = sisi a + sisi b + sisi c
= 13+5+12
= 30
Jadi, keliling segitiga tersebut adalah 30 cm.
Contoh Soal Keliling Segitiga:
Diketahui keliling sebuah segitiga adalah 64 cm. Tentukan panjang sisi ketiga jika diketahui panjang dua sisinya lainnya adalah 14 cm dan 24 cm!
Jawab:
Untuk menentukan panjang sisi sebuah segitiga jika diketahui keliling dan panjang dua sisi lainnya, kita dapat menggunakan rumus keliling segitiga sebagai berikut.
K = a+b+c
64 = 14+24+c
64 = 38+c
c = 64-38
c = 26
Jadi, panjang sisi ketiga dari segitiga tersebut adalah 26 cm.
Luas daerah pada sebuah segitiga adalah setengah dari hasil kali antara alas dan tinggi yang dimiliki oleh segitiga. Pada sebuah segitiga, alas adalah salah satu sisi dari segitiga. Namun sebenarnya, semua sisi bisa dijadikan sebagai alas. Sedangkan yang dimaksud tinggi adalah garis yang berpotongan tegak lurus dengan sisi alas.
Perhatikan gambar segitiga lancip di bawah ini.
Pada △KLM, KL dianggap sebagai alas (a) segitiga dan MN dianggap sebagai tingginya (t). Dengan demikian luas daerah untuk segitiga di atas dapat dirumuskan sebagai berikut.
a = alas
t = tinggi
Rumus luas segitiga ini berlaku untuk mencari luas semua jenis segitiga baik itu segitiga sama kaki, segitiga sama sisi, segitiga sembarang, segitiga siku-siku, segitiga lancip dan segitiga tumpul.
Contoh Soal Luas Segitiga:
Sebuah segitiga lancip memiliki panjang alas = 12 cm dan tinggi = 10 cm. Tentukan luas daerah dari segitiga tersebut!
Jawab:
Alas = 12 cm, maka a=12 cm.
Tinggi = 10 cm, maka t=10 cm.
L = 1/2×a×t
= 1/2×12×10
= 60
Jadi, luas daerah segitiga tersebut adalah 60 cm².
Contoh Soal Luas Segitiga:
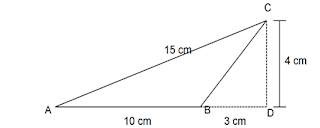
Sebuah segitiga siku-siku memiliki ukuran seperti gambar yang ada di bawah ini.
Tentukan luas daerah △ABC di atas!
Jawab:
Diketahui segitiga ABC memiliki:
Alas = 5 cm, maka a=5 cm.
Tinggi = 12 cm, maka t=12 cm
maka:
L = 1/2×a×t
= 1/2×5×12
= 30
Jadi, luas daerah segitiga tersebut adalah 30 cm².
Contoh Soal Luas Segitiga:
Perhatikan gambar segitiga tumpul berikut.
Tentukan luas daerah △ABC di atas!
Jawab:
Diketahui segitiga ABC memiliki:
Alas = 10 cm, maka a=10 cm.
Tinggi = 4 cm, maka t=4 cm
maka:
L = 1/2×a×t
= 1/2×10×4
= 20
Jadi, luas daerah segitiga tersebut adalah 20 cm².
Segitiga memiliki bentuk yang beragam. Dari keberagaman bentuk yang dimiliki, bentuk-bentuk segitiga itu dapat dibagi dalam beberapa jenis segitiga. Berikut akan dijelaskan jenis-jenis dari segitiga.
Jika kita melihat segitiga dari panjang sisinya, maka segitiga dapat dibedakan menjadi tiga jenis yaitu:
1. Segitiga sama kaki; segitiga yang memiliki dua sisi dengan panjang yang sama.
△ABC di atas merupakan contoh segitiga sama kaki karena memiliki dua sisi yang sama panjang. Sisi sisi tersebut adalah sisi AC dan sisi BC.
2. Segitiga sama sisi; segitiga yang memiliki tiga sisi dengan ukuran yang sama panjang.
Pada gambar di atas, △DEF merupakan contoh segitiga sama sisi karena ketiga sisinya berukuran sama atau bisa dituliskan DE = EF = DF.
3. Segitiga sembarang; segitiga yang memiliki tiga sisi dengan panjang yang berbeda-beda.
△FGH merupakan contoh segitiga sembarang karena ketiga sisinya memiliki panjang yang berbeda atau bisa dituliskan FG≠GH≠FH.
Jika kita melihat segitiga dari besar sudutnya, maka segitiga dapat dibedakan menjadi tiga jenis yaitu:
1. Segitiga lancip; segitiga yang ketiga sudutnya adalah sudut lancip. Dengan kata lain, semua sudutnya memiliki besar sudut kurang dari 90°.
△FGH merupakan segitiga lancip karena ketiga sudutnya yaitu ∠MKL, ∠KLM, dan ∠LMK adalah sudut lancip dengan besar sudut kurang dari 90°.
2. Segitiga siku-siku; segitiga yang salah satu sudutnya adalah sudut siku-siku. Dengan demikian, salah satu sudutnya memiliki besar sudut 90°.
Pada gambar di atas, △ABC merupakan segitiga siku-siku karena segitiga tersebut memiliki sebuah sudut siku-siku yaitu ∠ABC yang memiliki besar sudut 90°.
3. Segitiga tumpul; segitiga yang salah satu sudutnya adalah sudut tumpul. Dengan demikian, salah satu sudutnya memiliki besar sudut lebih dari 90°.
△DEF merupakan segitiga tumpul karena salah satu sudutnya (∠DEF) adalah sudut tumpul dengan besar sudut lebih dari 90°.
Misalkan dipunyai segitiga seperti gambar di bawah ini.
Jumlah besar sudut pada sebuah segitiga seperti pada gambar di atas adalah 180°. Pada △FGH dapat dituliskan bahwa ∠F+∠G+∠H=180°.
Contoh Soal Menghitung Besar Sudut Segitiga:
Besar sudut sebuah segitiga adalah 110° dan 45° . hitunglah berapa besar sudut yang ketiga!
Jawab:
Karena jumlah sudut segitiga adalah 180° , maka:
Besar sudut yang ketiga = 180°-( 110°+ 45°)
= 180° - 155°
= 25°
Jadi, besar sudut yang ketiga adalah 25°.
Nah demikian pembahasan lengkap mengenai bangun datar segitiga, mulai dari pengertian, rumus luas segitiga, rumus keliling segitiga dan jenis-jenis segitiga lengkap. semoga bermanfaat.[resky]
Pengertian Segitiga
Segitiga dapat didefinisikan sebagai berikut.
Segitiga adalah salah satu bangun datar yang dibatasi oleh tiga ruas garis dimana tiap dua ruas garis selalu berpotongan di satu titik.
Ruas-ruas garis yang terdapat dalam segitiga dikenal sebagai sisi-sisi segitiga. Adapun biasanya segitiga dilambangkan dengan “ △”. Perhatikan gambar di bawah ini.
- ∠A atau ∠BAC atau ∠CAB
- ∠B atau ∠CBA atau ∠ABC
- ∠C atau ∠ACB atau ∠BCA
Rumus Keliling Segitiga
Keliling segitiga adalah jumlah panjang dari ketiga sisi yang dimiliki oleh sebuah segitiga. Perhatikan △ABC di bawah ini.
Keliling △ABC = AB+BC+AC
K = sisi c + sisi a + sisi b
= sisi a + sisi b + sisi c
Dari hal tersebut, keliling dari sebuah segitiga dengan panjang sisi a cm, b cm, dan c cm dapat dirumuskan dengan:
Keliling Segitiga = sisi a + sisi b + sisi c
Rumus keliling segitiga ini berlaku untuk menghitung keliling semua jenis segitiga baik itu segitiga sama kaki, segitiga sama sisi, segitiga sembarang, segitiga siku-siku, segitiga lancip dan segitiga tumpul.
Contoh Soal Keliling Segitiga:
Tentukan keliling segitiga yang panjang sisinya 12 cm, 5 cm, dan 13 cm!
Jawab:
Diketahui panjang sisi segitiga adalah 12 cm, 8 cm, dan 10 cm, maka apabila digambarkan menjadi:
Keliling Segitiga = sisi a + sisi b + sisi c
= 13+5+12
= 30
Jadi, keliling segitiga tersebut adalah 30 cm.
Contoh Soal Keliling Segitiga:
Diketahui keliling sebuah segitiga adalah 64 cm. Tentukan panjang sisi ketiga jika diketahui panjang dua sisinya lainnya adalah 14 cm dan 24 cm!
Jawab:
Untuk menentukan panjang sisi sebuah segitiga jika diketahui keliling dan panjang dua sisi lainnya, kita dapat menggunakan rumus keliling segitiga sebagai berikut.
K = a+b+c
64 = 14+24+c
64 = 38+c
c = 64-38
c = 26
Jadi, panjang sisi ketiga dari segitiga tersebut adalah 26 cm.
Rumus Luas Segitiga
Luas daerah pada sebuah segitiga adalah setengah dari hasil kali antara alas dan tinggi yang dimiliki oleh segitiga. Pada sebuah segitiga, alas adalah salah satu sisi dari segitiga. Namun sebenarnya, semua sisi bisa dijadikan sebagai alas. Sedangkan yang dimaksud tinggi adalah garis yang berpotongan tegak lurus dengan sisi alas.
Perhatikan gambar segitiga lancip di bawah ini.
Luas segitiga = 1/2×alas×tinggi ⟹ Luas = 1/2 x a x tKeterangan:
a = alas
t = tinggi
Rumus luas segitiga ini berlaku untuk mencari luas semua jenis segitiga baik itu segitiga sama kaki, segitiga sama sisi, segitiga sembarang, segitiga siku-siku, segitiga lancip dan segitiga tumpul.
Contoh Soal Luas Segitiga:
Sebuah segitiga lancip memiliki panjang alas = 12 cm dan tinggi = 10 cm. Tentukan luas daerah dari segitiga tersebut!
Jawab:
Alas = 12 cm, maka a=12 cm.
Tinggi = 10 cm, maka t=10 cm.
L = 1/2×a×t
= 1/2×12×10
= 60
Jadi, luas daerah segitiga tersebut adalah 60 cm².
Contoh Soal Luas Segitiga:
Sebuah segitiga siku-siku memiliki ukuran seperti gambar yang ada di bawah ini.
Jawab:
Diketahui segitiga ABC memiliki:
Alas = 5 cm, maka a=5 cm.
Tinggi = 12 cm, maka t=12 cm
maka:
L = 1/2×a×t
= 1/2×5×12
= 30
Jadi, luas daerah segitiga tersebut adalah 30 cm².
Contoh Soal Luas Segitiga:
Perhatikan gambar segitiga tumpul berikut.
Jawab:
Diketahui segitiga ABC memiliki:
Alas = 10 cm, maka a=10 cm.
Tinggi = 4 cm, maka t=4 cm
maka:
L = 1/2×a×t
= 1/2×10×4
= 20
Jadi, luas daerah segitiga tersebut adalah 20 cm².
Jenis-Jenis Segitiga
Segitiga memiliki bentuk yang beragam. Dari keberagaman bentuk yang dimiliki, bentuk-bentuk segitiga itu dapat dibagi dalam beberapa jenis segitiga. Berikut akan dijelaskan jenis-jenis dari segitiga.
Jenis Segitiga Berdasarkan dari Panjang Sisinya
Jika kita melihat segitiga dari panjang sisinya, maka segitiga dapat dibedakan menjadi tiga jenis yaitu:
1. Segitiga sama kaki; segitiga yang memiliki dua sisi dengan panjang yang sama.
2. Segitiga sama sisi; segitiga yang memiliki tiga sisi dengan ukuran yang sama panjang.
3. Segitiga sembarang; segitiga yang memiliki tiga sisi dengan panjang yang berbeda-beda.
Jenis Segitiga Berdasarkan dari Besar Sudutnya
Jika kita melihat segitiga dari besar sudutnya, maka segitiga dapat dibedakan menjadi tiga jenis yaitu:
1. Segitiga lancip; segitiga yang ketiga sudutnya adalah sudut lancip. Dengan kata lain, semua sudutnya memiliki besar sudut kurang dari 90°.
2. Segitiga siku-siku; segitiga yang salah satu sudutnya adalah sudut siku-siku. Dengan demikian, salah satu sudutnya memiliki besar sudut 90°.
3. Segitiga tumpul; segitiga yang salah satu sudutnya adalah sudut tumpul. Dengan demikian, salah satu sudutnya memiliki besar sudut lebih dari 90°.
Jumlah Besar Sudut Segitiga
Misalkan dipunyai segitiga seperti gambar di bawah ini.
Contoh Soal Menghitung Besar Sudut Segitiga:
Besar sudut sebuah segitiga adalah 110° dan 45° . hitunglah berapa besar sudut yang ketiga!
Jawab:
Karena jumlah sudut segitiga adalah 180° , maka:
Besar sudut yang ketiga = 180°-( 110°+ 45°)
= 180° - 155°
= 25°
Jadi, besar sudut yang ketiga adalah 25°.
Nah demikian pembahasan lengkap mengenai bangun datar segitiga, mulai dari pengertian, rumus luas segitiga, rumus keliling segitiga dan jenis-jenis segitiga lengkap. semoga bermanfaat.[resky]
Labels:
Bangun Datar
0 Komentar untuk "Pembuktian Rumus Segitiga Luas Keliling Beserta Soal Dan Pembahasan Rumus Singkat Ilmiah"