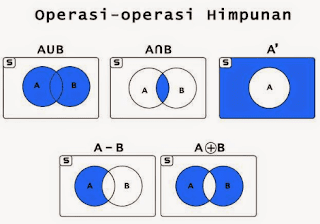
Operasi Himpunan Matematika - Jika terdapat dua himpunan atau lebih, maka kita bisa mengoperasikannya agar bisa memperoleh himpunan yang baru. Ada beberapa jenis operasi himpunan yang biasa digunakan seperti irisan, komplemen, gabungan, selisih, dan beda setangkup. Dalam artikel kali ini Belajar Matematikaku akan memberikan beberapa contoh soal mengenai operasi himpunan disertai dengan pembahasannya sehingga kalian bisa mempelajari langkah-langkah dalam menyelesaikan soal-soal tersebut. Langsung saja, perhatikan baik-baik uraian di bawah ini:
Tentukan A ∩ B!
Penyelesaian :
A = {1,2,3,4,5,6}
B = {1,3,5,7,9}
A ∩ B = {1,2,3,4,5,6} n {1,3,5,7,9}
A ∩ B = {1,3,5}
Jadi, A ∩ B = {1,3,5}
Contoh Soal 2: Diketahui himpunan P = {x | x ≤ 6, x bilangan cacah}, Q = {x| 1 ≤ x ≤ 8, x bilangan ganjil}, R = {x| 2 ≤ x ≤ 8, x bilangan asli} Tentukanlah P ∪ {Q ∩ R}!
Penyelesaian :
P = {0,1,2,3,4,5,6}
Q ={1,3,5,7}
R = {2,3,4,5,6,7,8}
Q ∩ R = {3,5,7}
P ∪ {Q ∩ R} = {0,1,2,3,4,5,6 } ∪ {3,5,7}
P ∪ {Q ∩ R} = {0,1,2,3,4,5,6,7}
Jadi, P∪ {Q ∩ R} = {0,1,2,3,4,5,6,7}
Contoh Soal 3: Diketahui himpunan A = {x| x ≤ 1, x bilangan asli}, himpunan B {x| x < 5, x bilangan cacah}.
Tentukanlah :
A – B!
Penyelesaian :
A = {1,2,3 dst…}
B = {0,1,2,3,4,5}
A – B = {1,2,3,4,5,6 dst…} - {0,1,2,3,4,5}
A – B = {6,7 dst..}
A – B = {x| x > 5, x bilangan asli}
Jadi , A – B = { x| x > 5, x bilangan asli}
Contoh Soal 4: Diketahui S adalah himpunan semesta. P dan Q merupakan himpunan bagian dari S. S = {e,u,r,a, s,i, h, o, m} . P = {r, a, o}, Q = {s,e,r, m,a}.
Tentukanlah (P ∪ Q)c!
Penyelesaian :
P ∪ Q = {r, a, o} u { s,e,r, m,a}.
P ∪ Q = {a, e, m, o,r, s}
(P ∪ Q)c = { u,i, h,}
Jadi, (P ∪ Q)c = { u,i, h,}
Contoh Soal 5: P = faktor dari 8, Q = bilangan cacah kurang dari 8. Tentukanlah P ∩ Q!
Penyelesaian :
P = {1,2,4,8}
Q ={0,1,2,3,4,5,6,7,8}
P ∩ Q = {1,2,4,8} ∩ {0,1,2,3,4,5,6,7,8}
P ∩ Q = {1,2,4,8}
Jadi , P ∩ Q = {1,2,4,8}
Itulah beberapa Contoh Soal Mengenai Operasi Himpunan Matematika dan Pembahasannya semoga kalian bisa memahaminya dengan baik dan semoga artikel ini bisa membantu kalian dalam menyelesaikan soal-soal yang berhubungan dengan materi ini.
Selamat belajar dan semoga bermanfaat!

Contoh Soal dan Pembahasan Operasi Himpunan
Contoh Soal 1: Diketahui Himpunan A = {x|x < 7, x bilangan asli}, B = {lima bilangan ganjil yang pertama}.Tentukan A ∩ B!
Penyelesaian :
A = {1,2,3,4,5,6}
B = {1,3,5,7,9}
A ∩ B = {1,2,3,4,5,6} n {1,3,5,7,9}
A ∩ B = {1,3,5}
Jadi, A ∩ B = {1,3,5}
Contoh Soal 2: Diketahui himpunan P = {x | x ≤ 6, x bilangan cacah}, Q = {x| 1 ≤ x ≤ 8, x bilangan ganjil}, R = {x| 2 ≤ x ≤ 8, x bilangan asli} Tentukanlah P ∪ {Q ∩ R}!
Penyelesaian :
P = {0,1,2,3,4,5,6}
Q ={1,3,5,7}
R = {2,3,4,5,6,7,8}
Q ∩ R = {3,5,7}
P ∪ {Q ∩ R} = {0,1,2,3,4,5,6 } ∪ {3,5,7}
P ∪ {Q ∩ R} = {0,1,2,3,4,5,6,7}
Jadi, P∪ {Q ∩ R} = {0,1,2,3,4,5,6,7}
Contoh Soal 3: Diketahui himpunan A = {x| x ≤ 1, x bilangan asli}, himpunan B {x| x < 5, x bilangan cacah}.
Tentukanlah :
A – B!
Penyelesaian :
A = {1,2,3 dst…}
B = {0,1,2,3,4,5}
A – B = {1,2,3,4,5,6 dst…} - {0,1,2,3,4,5}
A – B = {6,7 dst..}
A – B = {x| x > 5, x bilangan asli}
Jadi , A – B = { x| x > 5, x bilangan asli}
Contoh Soal 4: Diketahui S adalah himpunan semesta. P dan Q merupakan himpunan bagian dari S. S = {e,u,r,a, s,i, h, o, m} . P = {r, a, o}, Q = {s,e,r, m,a}.
Tentukanlah (P ∪ Q)c!
Penyelesaian :
P ∪ Q = {r, a, o} u { s,e,r, m,a}.
P ∪ Q = {a, e, m, o,r, s}
(P ∪ Q)c = { u,i, h,}
Jadi, (P ∪ Q)c = { u,i, h,}
Contoh Soal 5: P = faktor dari 8, Q = bilangan cacah kurang dari 8. Tentukanlah P ∩ Q!
Penyelesaian :
P = {1,2,4,8}
Q ={0,1,2,3,4,5,6,7,8}
P ∩ Q = {1,2,4,8} ∩ {0,1,2,3,4,5,6,7,8}
P ∩ Q = {1,2,4,8}
Jadi , P ∩ Q = {1,2,4,8}
Itulah beberapa Contoh Soal Mengenai Operasi Himpunan Matematika dan Pembahasannya semoga kalian bisa memahaminya dengan baik dan semoga artikel ini bisa membantu kalian dalam menyelesaikan soal-soal yang berhubungan dengan materi ini.
Selamat belajar dan semoga bermanfaat!


0 Komentar untuk "Kunci Plus Ulasan | Contoh Soal Operasi Himpunan Matematika Dan Pembahasannya -Lengkap Kisi Kisi UN/UNCU"