Rumus bangun ruang kubus - Kubus merupakan bangun ruang yang mempunyai panjang rusuk yang sama panjangnya serta merupakan bangun ruang tiga dimensi.
Perhatikan gambar kubus di bawah ini.
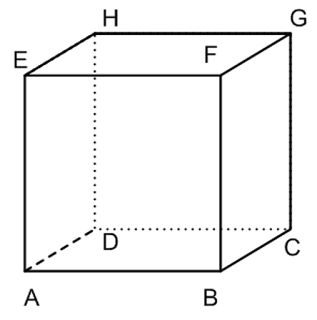
Setelah melihat gambar di atas kita bisa mengetahui jika :
1. Jumlah bidang sisi ada 6 buah yang berbentuk bujur sangkar yaitu ABCD, EFGH, ABFE, BCFG, CDGH dan ADEH.
2. Kubus mempunyai 8 buah titik sudut yakni A, B, C, D, E, F, G, H.
3. Memiliki 12 buah rusuk yang sama panjangnya yaitu AB, CD, EF, GH, AE, BF, CG, DH,AD, BC, EH, FG.
4. Mempunyai sudut yang semuanya siku-siku.
5. Mempunyai 4 diagonal ruang dan 12 diagonal bidang. diagonal ruang pada gambar diatas yaitu garis AG, BH, CE, DF sedangkan diagonal bidangnya yaitu garis AC, BD, EG, FH, DE, AH, CF, BG, AF, BE, DG dan CH.
Rumus Diagonal Sisi atau Diagonal bidang kubus = r√2
Rumus Diagonal ruang = r√3
Rumus Luas kubus = 6r2
Rumus Volume Kubus = r³
Perhatikan gambar kubus di bawah ini.
Setelah melihat gambar di atas kita bisa mengetahui jika :
Ciri-ciri kubus
1. Jumlah bidang sisi ada 6 buah yang berbentuk bujur sangkar yaitu ABCD, EFGH, ABFE, BCFG, CDGH dan ADEH.
2. Kubus mempunyai 8 buah titik sudut yakni A, B, C, D, E, F, G, H.
3. Memiliki 12 buah rusuk yang sama panjangnya yaitu AB, CD, EF, GH, AE, BF, CG, DH,AD, BC, EH, FG.
4. Mempunyai sudut yang semuanya siku-siku.
5. Mempunyai 4 diagonal ruang dan 12 diagonal bidang. diagonal ruang pada gambar diatas yaitu garis AG, BH, CE, DF sedangkan diagonal bidangnya yaitu garis AC, BD, EG, FH, DE, AH, CF, BG, AF, BE, DG dan CH.
Rumus Kubus
Rumus Diagonal ruang = r√3
Rumus Luas kubus = 6r2
Rumus Volume Kubus = r³
Panjang total kerangka = 12r
Rumus Diagonal Sisi/Diagonal bidang kubus = r√2
Sehingga rumus diagonal sisi selutuhnya = 12.r√2
Rumus Diagonal Ruang Kubus = r√3
Sehingga rumus diagonal ruang seluruhnya = 4.r√3
Luas Bidang Diagonal = r²√2
Sehingga Luas Bidang Diagonal Seluruhnya = 6.r²√2
( r adalah ukuran panjang rusuk )
Tulisan Terkait Tentang Kubus:
Pembuktian Rumus Volume Kubus Beserta Cara Menghitung Dan Soalnya Rumus Singkat Ilmiah
Pembuktian Cara Menghitung Luas Permukaan Kubus Lengkap Dengan Rumus Dan Soal Rumus Singkat Ilmiah
Baca juga artikel sebelumnya tentang Pengertian garis singgung lingkaran.
Demikian pembahasan tentang rumus kubus semoga menambah wawasan pengetahuan kita semua.()
Labels:
Bangun ruang,
Matematika SMP


0 Komentar untuk "Pembuktian Bangun Ruang Kubus : Rumus Dan Ciri-ciri Rumus Singkat Ilmiah"